
ギリシャの数学者ディオファントス
声に出してみたくなる名前ですね。ディオファントス。
彼は、方程式を研究し「代数の父」とよばれています。
『フェルマーの最終定理』でも数学を後世に残そうと奔走した様子が描かれていました。
ディオファントスの『算術』という本には、現在の x にあたる記号など、すでに言葉ではなく文字の記号を使った式も載っていました。
この『算術』の本が出版されたからこそ、あのピエール・ド・フェルマーがフェルマーの最終定理(まだ当時は予想ですね)を書き記すことができたのですから、胸熱です。
そうした、数学者達のストーリーを飽きずに描いたのが『フェルマーの最終定理』です。この本を含めて数学の本を紹介した記事もあるので、もしよければチェックしてみてください。
| 【数学×小説】現役数学教員がおすすめする数学小説3選 |
さて、今日はそのディオファントスについて、有名な問題を紹介します。
内容は、中学1年生「1次方程式」で解くことができるので、子どもに解かせてみても面白いかもしれません。
ディオファントスの墓碑銘
ディオファントスのお墓には「彼は何歳生きたか?」という問題が記されているそうです。
ディオファントスの人生は、6分の1が少年期、12分の1が青年期であり、その後に人生の7分の1が経って結婚し、結婚して5年で子供に恵まれた。ところがその子はディオファントスの一生の半分しか生きずに世を去った。自分の子を失って4年後にディオファントスも亡くなった。
では、この問題を1次方程式として考えていきましょう。
解法
まずは、方程式を解く手順を確認します。
|
この手順に沿って考えていきましょう。
求めたいものを未知数 x で表す。
求めたいものはもちろんディオファントスが何歳生きたかです。
したがって、ディオファントスが生きた年齢を x とします。
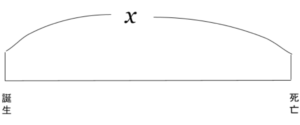
x を使って、数量の関係を文字式で表し、文章にそって、方程式をたてる。
x を使って、数量の関係を文字式で表すと、
$$ 少年期は、 \frac{1}{6} x $$
$$ 青年期は、 \frac{1}{12} x $$
$$ 結婚したのは、 \frac{1}{7} x $$
$$ 子どもが生まれたのは、 \frac{1}{7} x の5年後 $$
$$ 子どもの生涯は、 \frac{1}{2} x $$
$$ 死亡したのは、 \frac{1}{2} x の4年後 $$

すべての数を足すとディオファントスの年齢 x になるので式は次の通りになります。
$$ \frac{1}{6} x + \frac{1}{12} x + \frac{1}{7} x + 5 + \frac{1}{2} x + 4 = x $$
方程式を解く。
方程式を分数に注意しながら解きます。
両辺に12をかけてまとめる。
さらに両辺に7をかけてまとめるのがやりやすいですね。
どのように解いても、解は84となります。
方程式の解が問題に適しているかどうかを確かめる。
84歳というのはおかしな数ではないので、このまま答えとしてよさそうです。
答え:84歳

最後に
以上ディオファントスの墓碑銘の問題を紹介しました。
分数が絡んでくるので、1年生の方程式としても扱っても練習になると思います。
また、よくよく考えると、7と12の公倍数で一番それらしいものを選べば答えを予想することもできてしまいます。割り切れないわけないですからね。
過去の数学者の逸話や功績はストーリーとしてとても魅力的です。
今の数学ができあがるまでに、どれほどの天才達が知識を積み上げてきたかを知るだけでも人生にとってプラスになると思います。
特に『フェルマーの最終定理』はおすすめです。
この一冊で紀元前から現代までの有名な数学者について知ることができます。
数学が苦手な方でも読み物としても優秀なのでスラスラ読むことができます。
気になる方はチェックしてみてください!
| 【数学×小説】現役数学教員がおすすめする数学小説3選 |























