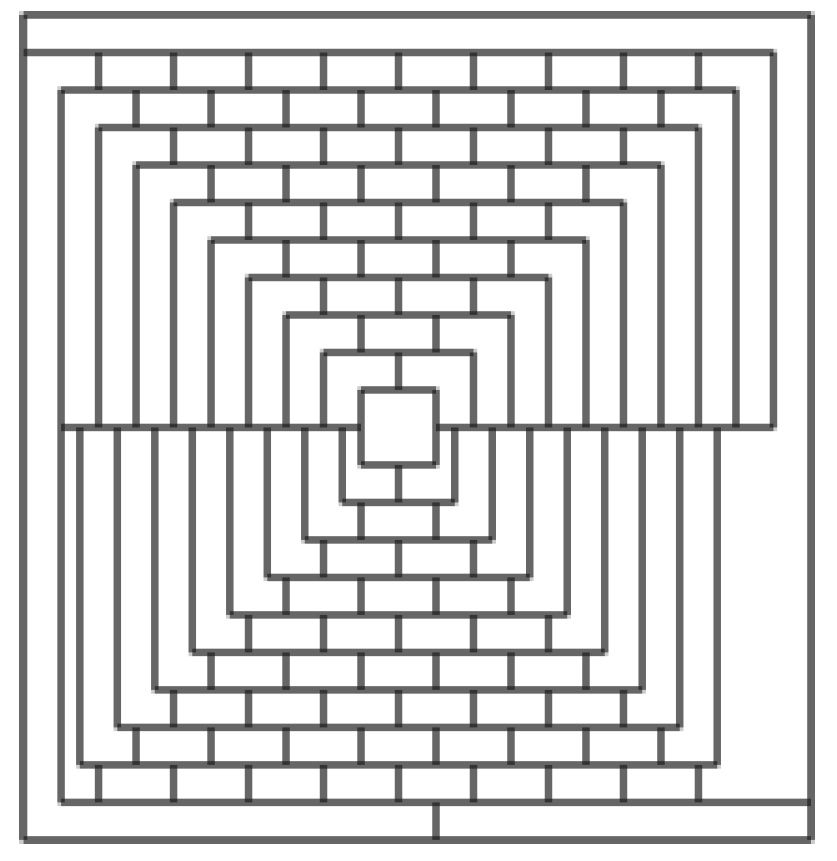
今回は「マクレガーの地図」という題材を紹介します。
マクレガーの地図を説明する前に前提となる知識があります。
【四色定理】
四色定理とは、簡単に言うと、
どんな地図でも色が四色あれば塗りきることができますよってことです。
もちろん、境界線を越えて同じ色はダメです。
例えば下の図形で考えてみましょう。
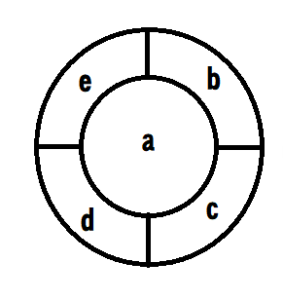a,b,c,d,eと五つの領域があります。
このとき、赤、青、黄、緑を塗るとします。
aに赤を塗るとb,c,d,eには隣り合っているので赤を塗ることができません。
さらに、bに青を塗るとe,cには赤と青は塗れません。
c,eにそれぞれ黄、緑を塗るとdには何色を塗ることができるでしょうか。
・・・そうですね、dにはbと同じ青を塗ればよいですね。
結果このようになります。単純ですね。
四色定理について、Wikipediaによると
「平面上のいかなる地図も、隣接する領域が異なる色になるように塗り分けるには四色あれば十分だ」という定理です。
以上四色定理の説明でした。
そして、その四色定理に対しての反例ができたぞーっていうのが下の「マクレガーの地図」です。
（反例というのは、この定理が成り立たない具体的な例のことです。）
マクレガーの地図は、昔エイプリルフールに四色定理の反例として数学雑誌に掲載された問題です。
この地図は本当に四色で塗りきることはできないのか・・・？
いえいえ、これはエイプリルフールの記事です。
ちゃんと四色で塗りきることができます。
では、実際に塗ってみましょう。
マクレガーの地図PDFなのでよろしければチャレンジしてみてください！！
コツは最初から色を塗るのではなく、番号や記号で仮決定していくことです。
行き当たりばったりではうまくはいきません。頑張りましょう。
これは数学の問題なので証明することもできます。
しかし、その証明方法もコンピュータを利用して総当たりする「ごり押しの証明」なので
証明は割愛します。（詳しくはWikipediaをご覧ください）
ちなみに自分でやった完成形はこちらです。
今回の問題は数学の授業としては扱いづらいので学期末の空いた時間などに息抜きとして子ども達にやらせてみると良いかもしれませんね。
中学校１年生～３年生までどの学年でも熱中して色塗りします。（笑）
ちなみにちなみに・・・
四色定理は携帯電話の基地局に応用されています。
定理の「地図」を「基地局」に置き換えて考えます。
隣り合う基地局で同じ周波数の電波を使うと混信していまいます。
しかし、四色定理を応用し隣り合う基地局では異なる電波を使うようにすれば混信することがありません。
以上、最後まで読んでいただきありがとうございました。
