

今日はそんな疑問に答えます。
小学校6年生の算数、中学校1年生の数学の履修範囲に入っている「代表値」
「〇〇値」というのがいくつも出てきて区別がつかないとか、どういうときに何値を使えばいいかわからないという人のために参考になれば嬉しいです。
代表値とは、資料の傾向を一発で説明するもの
そもそも、代表値とは何でしょうか。
総務省によると、
集団の中心的傾向を示す値を「代表値」といいます。
総務省統計局
要するに、データの傾向を「代表」する「値」ということです。
よく使われるのが「平均値」
例えば、Aさんの5教科のテストの結果が、
国語:90点 数学:100点 理科:50点 社会:70点 英語:90点
だとすると、このときの平均点は80点となります。
(90+100+50+70+90)÷5=80
この80点というのは、Aさんの学力を代表している値と捉えることができます。
だから、

となるわけです。
知っておくべき代表値は、「平均値」「中央値」「最頻値」の3つ!
では、学校で学ぶ代表値にはどのようなものがあるのでしょうか。
最大値や最小値など似ているような「〇〇値」はあるのですが、学校で学ぶ代表値は、
「平均値」「中央値」「最頻値」
これら3つです。
平均値(アベレージ)
平均値は、上のテストの例で出したように、一番身近にある代表値です。
とても使い勝手がよく、理解している人も多いはずです。
ちなみに求め方は、
資料(データ)のすべての数値の和を個数で割ったものです。
$$ 平均値= \frac{資料のすべての数値の和}{個数の合計} $$
中央値(メジアン)
中央値は、資料を、その値の大きさの順に並べたとき、中央にあたる値のことです。
資料の個数が奇数個の場合は、そのまま中央の値。
資料の個数が偶数の場合は、中央に並ぶ2つの資料の平均値になります。
【奇数個のとき】
1、2、2、3、4、4、9
このとき中央値は、中央の3。
【偶数個のとき】
2、2、3、4、4、9
このとき中央値は、中央の3と4の平均の3.5。
個数が、偶数個のときに注意が必要です。
中央値より小さい値と大きい値が同じ個数になることも特徴の一つです。(当たり前ですが。)
また、学校の問題で間違えやすいのは、資料の個数を大きさの順に並び替えないで中央値を答えてしまうことです。
例えば、次のような問題があったとします。
Q:10点満点のテストの結果が次のようになりました。中央値を求めなさい。 4点、8点、2点、6点、9点、10点、7点
このとき答えは何になりますか?
答えは、7点ですよね。
並び替えないと、6点と答えてしまうので気をつけましょう。
最頻値(モード)
最頻値は、(最)も(頻)度が高い(値)のことです。
要するに、資料のそれぞれの個数を数えて一番多いものが最頻値となります。
クラスの中で、一週間に借りる本の冊数を調べたら、次のようになった。
3冊、5冊、6冊、0冊、3冊、0冊、1冊、1冊、3冊、4冊、3冊、2冊、2冊
このとき、最頻値は3冊。
上の例で、3冊借りている人が4人いるから、4と答えたり、一番多い冊数が多いから6と答える間違いが多いので気をつけましょう。
中央値と最頻値はハズレ値があるときに使う!

平均値の他に、中央値と最頻値があることは分かったけど、こんなの使うの?
平均値だけでいいじゃん!
実は、とても便利な平均値ですが2つ弱点があるのです。
それは、
- ハズレ値に大きく影響を受けてしまうこと
- 実態がない可能性があること
もう少し詳しく説明していきます。
ハズレ値に大きく影響を受けてしまうこと
ハズレ値とは、その資料の中で極端にかけ離れた値のこと。
その資料の中に極端にかけ離れた値があると、平均値はその影響を大きく受けてしまいます。
例えば、激ムズのテストがあり、Bさんだけ猛勉強してきて高得点を取ったとします。すると、次のような資料(データ)になります。
90点(Bさん)、10点、5点、10点、4点、10点、5点、10点、6点、10点
このときの平均点は16点となります。
(90+10+5+10+4+10+5+10+6+10)÷10=16
この16点というのは、資料全体の傾向を表しているとは言いづらくなってしまいます。
Bさん90点というハズレ値の影響です。
このようなときに便利なのが、中央値です。
中央値はハズレ値の影響を受けません。
上の例だと、中央値は10点となり、10人の中で5人も10点の生徒がいますから、資料の傾向としても適しているといえますね。
実態がない可能性があること
誤解を恐れずに言うと、平均値は資料の合計を個数で割って求めるだけのただの計算結果です。
ですから、そこから生まれた値に実態が伴っていないこともあります。
例えば、上で紹介したAさんのテストの例をもう一度見てみましょう。
例えば、Aさんの5教科のテストの結果が、
国語:90点 数学:100点 理科:50点 社会:70点 英語:90点
だとすると、このときの平均点は80点となります。
(90+100+50+70+90)÷5=80
この80点というのは、Aさんの学力を代表している値と捉えることができます。
これを見てあることに気付きませんか?
80点という点数は、Aさんのどの教科にもありません。
別の例を示します。
次の資料は、ある靴屋さんで1週間に売れたサイズです。もっと売り上げを伸ばすためには何cmの靴を仕入れればよいでしょうか。
22cm:1足 23cm:6足 24cm:5足 25cm:1足 26cm:0足 27cm:1足 28cm:3足 29cm:3足
このとき平均値は、
(22×1+23×6+24×5+25×1+26×0+27×1+28×3+29×3)÷20=25.15
この平均値25.15cmから、25cmの靴を仕入れた方がよいですか?
25cmの靴は1週間で1足しか売れてませんから、適していないことがわかりますね。
このような場合、実態が伴うようにするためには最頻値がとても有効。
単純に一番売れているサイズ、つまり23cmや24cmを仕入れればいいことになります。
最後に・・・誤解されやすい平均値
今日は、代表値についての説明と、どんなときにどの代表値を使えばいいかを紹介してきました。
少しでも、理解が進んでくれれば嬉しいです。
最後に、もう一つ代表値に平均値が合わない例を紹介しましょう。
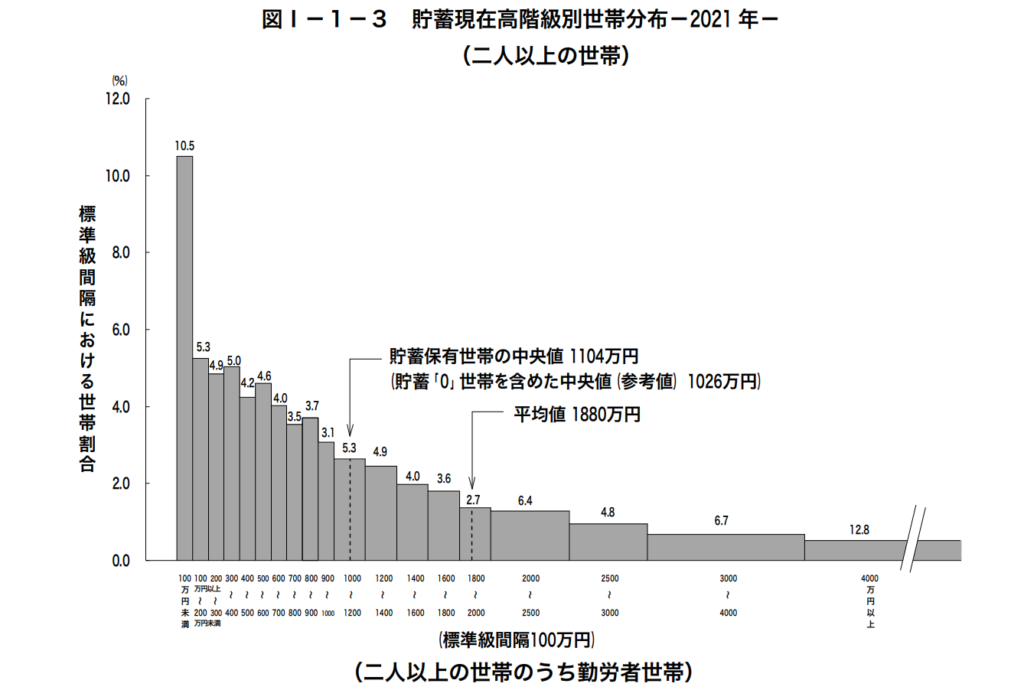
総務省統計局がまとめた令和3年度の貯蓄動向調査によると、日本の勤労者世帯の平均貯蓄高は1880万円です。この値が一般の家庭の感覚と合わないのは上で述べた通りですよね。
実際に平均値を下回る世帯は全体の約67%をしめ、貯蓄の低いほうに偏った分布をしています。
貯蓄高が3000万円以上の世帯が19.5%ということが、平均値に影響を与えていることがわかりますね。
このデータを見るときにも、やはり中央値の1026万円や最頻値の100万円未満のほうが現実に合ったといえますね。
また、他の分野の数学について興味がある人には、数学の小説がおすすめです!
特に、僕が好きなのは『フェルマーの最終定理』
過去の数学者の逸話や功績がストーリーとして語られているとても魅力的です。今の数学ができあがるまでに、どれほどの天才達が知識を積み上げてきたかを知るだけでも人生にとってプラスになると思います。
この一冊で紀元前から現代までの有名な数学者について知ることができます。数学が苦手な方でも読み物としても優秀なのでスラスラ読むことができます。
気になる方はチェックしてみてください!












