
3月は別れの季節で、4月は出会いの季節です。
中学校3年生の担任をしていると3月と4月の心持ちはかなり違ってきますよね。
3月は生徒が自分から離れていき、4月は自分へ近づいていく。
なかなか、感慨深いですね。
このとき、離れていく生徒より残された自分の方が寂しいと思うことはありませんか?
離れていく生徒はゆっくり歩いているのに、それを見ている自分は、あっという間に生徒が小さくなっていくような感覚におちいります。
今日は、このことについて相似の考えを使って考えていきましょう。
別れて歩いていく人が急に小さく見える理由
では、人と別れる時に相手が自分からゆっくり離れていくと急に小さく見える理由について考えていきます。
前提
以下を前提とします。
- 位置関係は自分の前に生徒がいる。
- 生徒は一本道をまっすぐにゆっくりと歩いていくとする。
- 自分は、立ち止まってずっとその生徒を見届けている。
- 自分は、生徒を長い物差しを通して見ているとする。
- 自分は、腕をまっ直ぐ伸ばして、物差しを地面と垂直方向に立てて持っている。
図にすると↓のような感じです。(絵心がないのは気にしないでください笑)
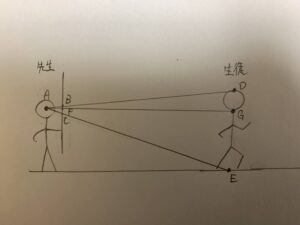
相似の考えを使ってみよう!
上の絵の状況で、先生の目の位置をA、生徒の頭の上の位置と靴の位置をそれぞれD、E、先生が物差し上で見る生徒の頭上の位置と靴の位置をそれぞれB、Cとし、Aを通る生徒への水平な直線と物差し、生徒との交点をそれぞれF、Gとして、図を書き直します。
それがこちら、
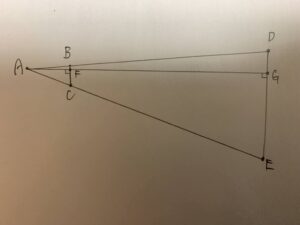
この図で考えていきます。
△ABCと△ADEにおいて、BC//DEであるから、
∠ABC=∠ADE
∠ACB=∠AED
より、2組の角がそれぞれ等しいので、
△ABC∽△ADE
となります。
同様にして、
△AFC∽△AGE
となります。
これらにより、
BC:DE=AC:AE
AF:AG=AC:AE
が成り立ちます。
ゆえに、
BC:DE=AF:AG
が導かれます。
内項の積と外項の積は等しいので、
BC:DE=AF:AG
BC×AG=DE×AF
∴ BC=(DE×AF) / AG
が導かれます。
この式で、DEというのは生徒の身長、AFは先生の目と物差しの間の距離なので、定数となります。
したがって、先生が物差し上で見る生徒の身長BCは、先生から生徒までの距離AGに反比例することがわかりました。
具体的に考えてみましょう。
AF=45cm、DE=170cm、AG=12.75m=1275cm
のときは、
BC=170×45÷1275=6(cm)
となります。
つまり、12.75m離れただけでも、先生から生徒を見ると、生徒の身長は6cmになってしまうということです。
これなら確かに、残された側の方が寂しい思いをしてしまうのは仕方ありませんね。
まとめ
以上が別れて歩いていく人が急に小さく見えてしまう理由となります。
内容としては中学校3年生の相似を学習した後なら理解できると思います。
内容の具体性、相似の証明をしてからの数値の代入など、授業の中で扱ってみても面白いかもしれませんね。
それではまた!
最後まで読んでいただきありがとうございました。
こちらもどうぞ!













