
こんにちは、今日は中学校一年生の方程式で使える数学ネタを紹介します。
今回紹介するのは、「トランプを使った天びん問題」です。
方程式の導入としても使えますし、移項や等式の性質の学習にも最適です。
トランプを使ったネタは、よく正の数・負の数でも取り入れている先生も多いと思います。
なので、子ども達にとっても受け入れやすネタです。

と思えれば、後々の授業もやりやすくなりますよ!
では、具体的にみていきましょう!!
トランプを使った天びん問題
目的
今回の問題では、以下のことを目的とします。
- トランプを使うことで、抵抗感なく方程式の問題に取り組ませる
- 等式の性質を直感的に理解する
- 移項の考え方を身につける
準備物
黒板とチョークだけでもOKですが、 ↓ のような大きいサイズのトランプがあると便利です。百均とかでも売ってるかもしれません。
または、大きめの画用紙に手書きしましょう。

僕は大きいサイズのトランプを持っています!
数学ってトランプ使うこと多いですよね!
授業の流れ
授業の流れは、大まかにいうと、次のようになります。もちろん先生のやりやすいように変更可能です。
- トランプでの計算練習
- 天びんを使った例題①
- 天びんを使った例題②
- 問題作り
- まとめ
詳しく解説していきます。
トランプでの計算練習
授業の導入では、トランプを使っての計算練習をします。
「正の数・負の数」でトランプを使った計算練習をしている場合は、簡単に確認するだけでOKです。
トランプには黒のカード(スペード・クローバー)と赤のカード(ハート・ダイヤ)があります。
黒いカードが正の数、赤いカードが負の数として考えます。
以下が例です。
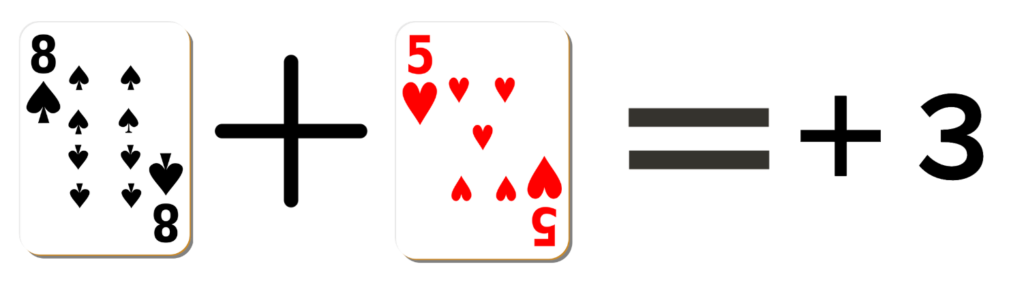
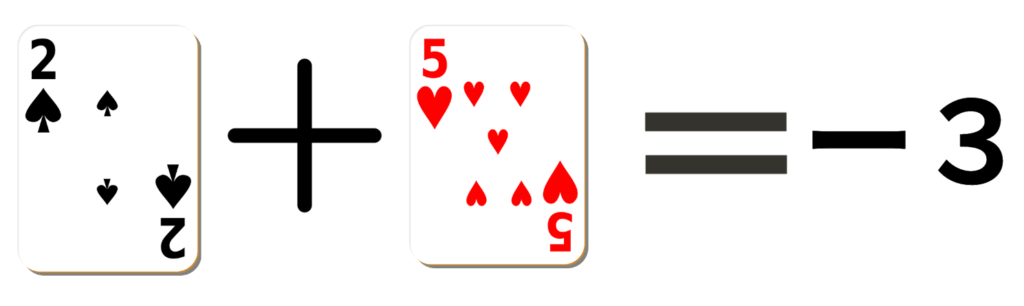
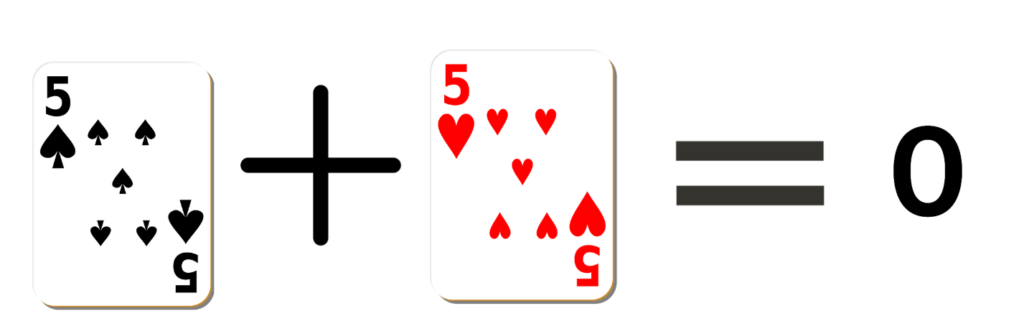
天びんを使った例題①
続いては天びんを使った例題です。
以下の天びんがつり合っているとき、「?」はいくらかを考えます。
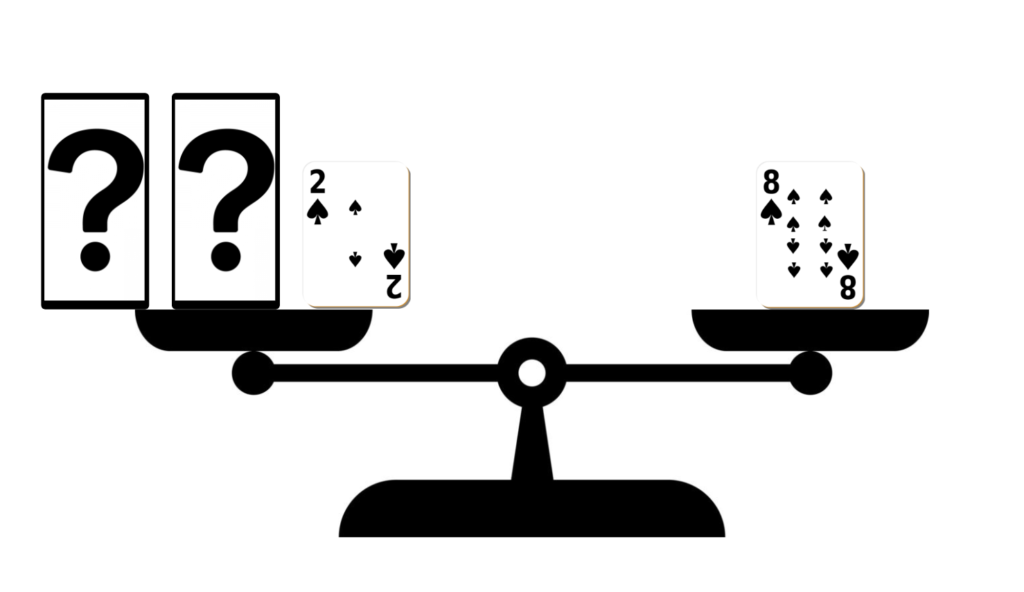
直感で「+3」だとわかる子もいるかもしれませんが、天びんの特徴と等式の性質を対応させるために丁寧に考えていきます。

天びんは、両方の皿から同じ数を乗せても取り除いてもつり合いは変わりません。
この性質を利用すると「?」はいくらになるでしょうか。



今の状態から、数字がわかっている「+2」を取ってもつり合います。
すると、左の皿は「?」が2枚、右の皿は「+6」になります。
「?」が2枚あるから、両方の皿を2等分すると「?」は「+3」になります。

子どもが発表するのに合わせて、黒板のトランプを張り替えると他の子もわかりやすくなります。
天びんを使った例題②
続いてもう一題出して個人で考えさせます。
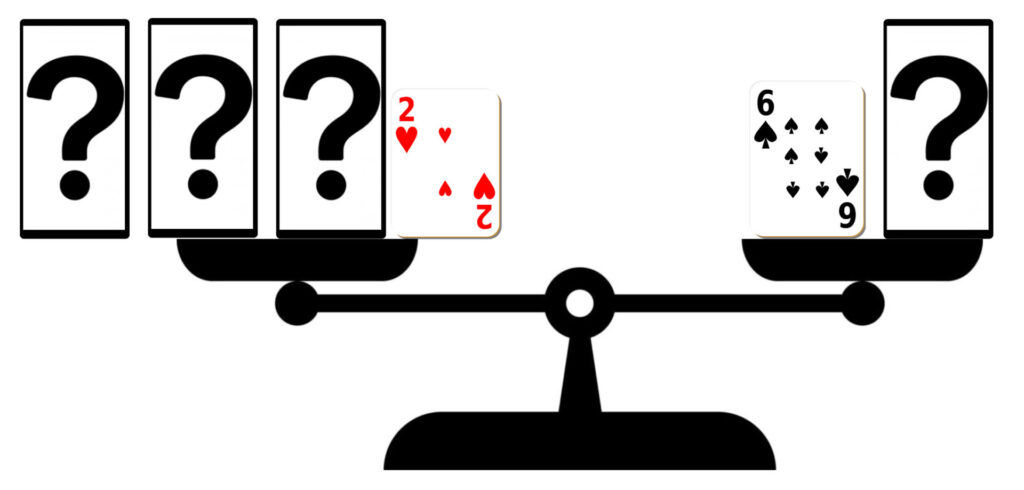
左の皿の「−2」を取り除くためにはどうすればよいかを考えさせます。
「−2」を取り除くためには、両方の皿に「+2」を加える、つまり、どちらかの皿からカードを取り除くためには、もう一方の皿に符号を変えた数を加えることに気づかせます。(移項の考え)



まずは、左の皿を「?」だけにしよう!


「−2」を「0」にするには、「+2」が必要だな〜。
つり合ったままにするには…わかった!
両方の皿に「+2」を加えればいいんだね!

すると、左の皿には「−2」と「+2」があるから「0」になる。
だから、結局は右の皿だけに「+2」を加えればいいね!


あとは簡単!両方の皿から「?」を1枚ずつ取る。
すると、左の皿は「?」が2枚、右の皿は「+8」になる。
1問目と同じように2等分すれば「?」は「+4」だ!
問題作り
例題ができたら自分たちで問題を作り、ペアで解かせます。
問題の作り方は先生のやりやすいようにやってください。
ノートに書かせてもいいですし、実際のトランプを渡してもOK。
ICTを使っても簡単に作れます。
先生は机間指導しながら、問題の天びんがつり合っているかどうかを確認します。
まとめ
一生懸命に取り組んでくれた子どもたちを褒めましょう。
特に、数学が苦手な子も一生懸命考えている姿があれば認めてあげることが大切です。
方程式は中学校3年間毎年学ぶことになるので、1年生のうちから

方程式って結構簡単じゃん
と思わせておくのが吉です。
最後にまとめをします。
等式の性質や移項の考えを改めて確認して授業終了です。
なにかしら参考になれば幸いです。
数学とトランプは相性がいいので大きいサイズのトランプを用意しておくと何かと便利です。
また、他の分野の数学について興味がある人には、数学の小説がおすすめです。
特に、僕が好きなのは『フェルマーの最終定理』
過去の数学者の逸話や功績がストーリーとして語られているとても魅力的です。今の数学ができあがるまでに、どれほどの天才達が知識を積み上げてきたかを知るだけでも人生にとってプラスになると思います。
この一冊で紀元前から現代までの有名な数学者について知ることができます。数学が苦手な方でも読み物としても優秀なのでスラスラ読むことができます。
気になる方はチェックしてみてください!













